As the shuttle flies: The physics of the badminton projectile

Ever wondered how a badminton shuttlecock flies?  This Badzine special feature takes a scientific look at the flight of the shuttle through the magic of computational fluid dynamic simulation.

By Denis Vuillemin, Badzine Special Contributor

Perhaps most of you are more or less faithful badminton players who have been joyfully practicing and passionately reading Badzine about the game. So am I. But have you ever wondered how that curious thing, the badminton shuttlecock, flies?  If you think that looking at this badminton question from a scientific point of view sounds interesting, take some time (and maybe have some aspirin handy) to read a few lines which will bring you a new vision of your flying shuttlecock!

CFD? What’s that?

Any time you watch a weather forecast on TV, you have, no doubt, been shown those maps with curious moving lines and vortexes.  Would you ever have thought that you could apply that type of model to a badminton shuttlecock?  Well, I decided to merge my two oldest passions: aerodynamics and badminton. As a student of aeronautical engineering, I figured I could investigate with my means and my knowledge on my own to finally visualize what’s happening around a shuttle during its flying motion.

Now, in the case of using the same science for meteorological forecasts, the science can be imprecise, particularly when one is trying to predict the weather a week in advance.  But let me explain you how it does work, on a shuttlecock.

The equations in fluid mechanics (the science of fluids, liquids and gas motion) are very complicated, so complicated that it would take several weeks for a human to solve one in a complex geometry such as a shuttle. In such cases, we use computational fluid dynamics (CFD), to predict what will happen, just like meteorologists do.  This means that the space is divided into millions of very tiny cells and every fluid mechanics equation is solved by a supercomputer for very short time increments.

For example, imagine I’d like to predict the flow behaviour around a shuttle over the course of even just one tenth of a second. If my space model is divided into 10 million cells, and my time increment is 10µs (0.00001s), then the supercomputer will solve the 10 million CFD equations on ten thousand different time ‘periods’.  Then there are 2 main equations in fluid mechanics, for each of the 3 dimensions of space, which make a total of… let’s see…

10 million x 10,000 time step x 2 equations x 3 dimensions = 600 billion equations!

Sorry… It would take generations for human to solve that. That’s why we leave that job to supercomputers, just like those used for meteorological forecasts or nuclear prevention scenarios.

I will not explain the entire theory of fluid mechanics due to its complexity, but if you’re interested you will find the 2 governing equations (the Navier Stokes equation and the mass conservation equation) here.

Modeling a virtual badminton shuttlecock

Let’s begin. Engineers have come up with some fantastic computing tools for three-dimensional conceptualization to create virtual designs with expensive or complicated geometries before actually trying to build them with real

materials. I designed my virtual badminton shuttlecock on computer-aided-design software  such as that used to design famous aircraft like the Airbus A380 or the Rafale fighter jet.

Just with my ruler, compass and protractor I measured the real dimensions of a classical feather shuttlecock. I successfully designed the cork, the collars, and then, placed the feathers inside, just like in real life.

I acknowledge that I’m not really an expert yet; thus, as a first model, the shuttle is considered as inflexible, and feathers are solid (not porous). Moreover, the spinning motion of the shuttle will not be studied with this model.

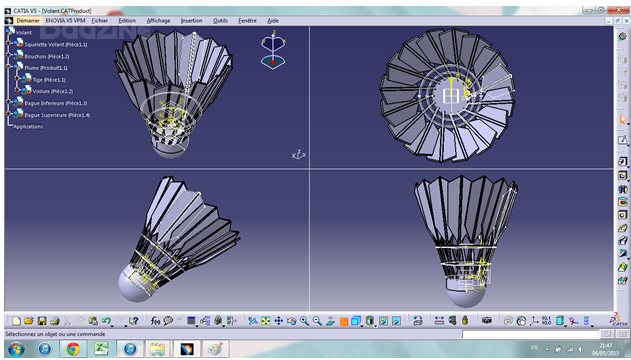
The meshing (dividing surfaces and space) procedure is quiet complicated. An example of the shuttle mesh is shown below:

The surface of the shuttle is divided into very small cells (around 0.1mm) whereas the rest of the space will be affected with larger cells. Of course, the higher the number of cells, the more accurate the calculation. But of course, the greater the accuracy, the longer and more expensive the calculation, too! But once the mesh is ready, actually with 75 million cells, the model can be exported into supercomputers in order to run the simulations.

Simulation Results

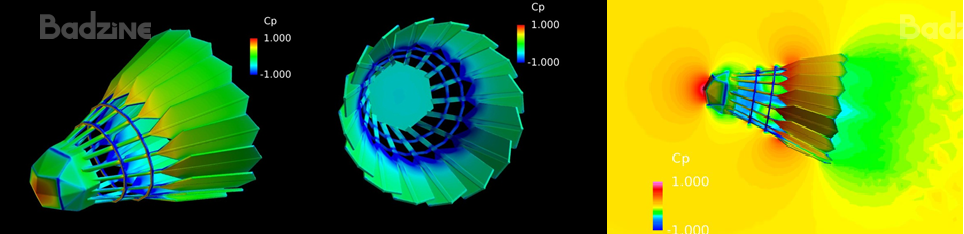
I decided to run the simulation with a constant velocity of 250km/h – the speed of an above-average professional badminton smash – to visualize how the flow acts on the shuttle during its motion.

Cp is called coefficient of pressure, the higher it is, the higher the pressure applied on the area. An interesting thing to see is that the biggest pressure is applied on the cork and in the bottom of feathers. Indeed, in the cork, the Cp has a value of 1, which means it’s a stagnation point: the flow stops exactly at this point! Moreover, the high pressure applied on the feather base, (meaning high aerodynamic forces) might explain why our shuttles tend to break suddenly so often on this part, leaving a big gap between the two adjacent feathers! Actually, the pressure is very high outside the feathers, and very low inside them, which yields to very strong aerodynamic forces, applied from outside to inside the shuttle.

The table below summarizes the repartition of aerodynamic forces on a shuttlecock as Drag (Trainée), Lift (Portance) and Side force (force latérale):

Suddenly, we understand why once the shuttle loses a bunch of feathers; it simply becomes an unstoppable rocket! Almost no more forces are applied if feathers are broken. And as lift and side force are negligible compared to drag, we understand there why, a shuttle, is definitely bound to slow down very quickly. Indeed, all feathers undergo a force of 4N, which approximately represents a weight of 400 grams (remember that since a shuttle weighs only 5 grams, it’s tantamount to a human holding off an African elephant!)

Inside Velocity Animation with mesh:

Outside Velocity Animation:

Here are interesting views of the velocity of the flow outside the shuttlecock, and inside it. The animation is more beautiful that useful, but we can easily see there the huge drag yielded by the feathers: the velocity is much reduced in the wake of the shuttle due to its feathers.

Some of you have noticed the absence of vortexes in the wake of the shuttle. Of course, the turbulence is so huge at 250km/h that there are many vortexes!

But for this simulation, I used a calculation method called LES (Large Eddy Simulation), which averages the equations and shows only the main flow and cancels micro perturbations and vortexes.

Moreover, we can see inside the shuttle that the flow is very unstable, even if it’s not spinning here. Needless to say, if one feather is changed, the whole flow inside the shuttle and consequently its trajectory will be changed. That’s why our favourite badminton superstars love changing shuttlecock every 2 points!

An idea of the turbulence explicated can be visualized on the animation below, where we can clearly see that it’s a pretty mess inside the shuttle! This animation is showing all the properties explained before and can summarize the whole behaviour of a steady shuttlecock during its motion.

Turbulence and velocity field animation:

Well, that’s it for a first public scientific approach of aerodynamics, applied to the badminton shuttlecock. I’m very sorry if you’ll have a headache all the day now… But just imagine there are many things that can be improved in my model: implement the spinning motion, simulate a feather break… Broadly, science will always be busy, and even a simple shuttlecock can be a whole lifetime of research!

Please share but do not copy.

© Denis Vuillemin. All rights reserved.